Grok 4’s Math Capabilities
An assessment of math capabilities beyond headline numbers
xAI commissioned us to analyze Grok 4’s math capabilities. Our findings:
+ It’s good at involved computations, improving at proofs (from a low base), and useful for literature search.
- It favors low-level grinds and leans on background knowledge.
Grok 4 set a new record on high school math competitions with short-form numerical answers. Here is one problem Grok 4 solved that no other model has solved.
Whereas the human reference solution is quite conceptual, Grok 4 approaches it via coordinate geometry and calculus. This “grind it out” style is typical of LLMs.
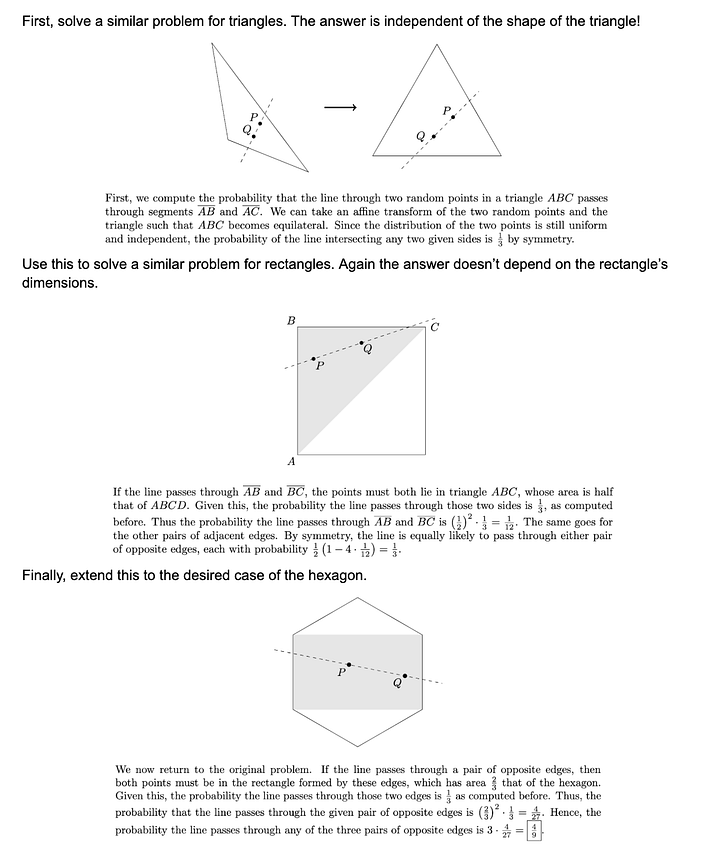

Such benchmarks are very nearly saturated. Going forward, the most interesting thing we can learn from them is whether models start to solve these problems in more conceptual ways. Grok 4 doesn’t indicate any change on this front.
Grok 4 also improved at proofs. Below is a competition problem which, among all models, Grok 4’s “Heavy” mode comes closest to solving. Its solution is not “from scratch”, however, but relies on extensive background knowledge.
Much headroom remains here. Grok 4 did not shine on the IMO, a more recent proof-based competition. It also seems to be less capable when deep background knowledge is less relevant. Like all LLMs, its attempted proofs can contain hard-to-spot logical flaws, hampering utility.
We also worked with two professional mathematicians to evaluate Grok 4’s capabilities. Both were impressed with Grok 4’s ability to search the mathematical literature, although they emphasized that it should be used with care.


Overall, Grok 4’s progress is more incremental than revolutionary. This suggests that "RL at pretraining scale" does not immediately deliver AI systems capable of doing a mathematician’s job.
See the full report on our website for more insights.





